言語モデルの感情バイアスの評価と除去

タイトル： Reducing Sentiment Bias in Language Models via Counterfactual Evaluation
著者： Po-Sen Huang, Huan Zhang, Ray Jiang, Robert Stanforth, Johannes Welbl, Jack Rae, Vishal Maini, Dani Yogatama, Pushmeet Kohli
会議・出版： EMNLP Findings
年： 2020

💡 概要

• 言語モデルによって生成されたテキストの感情バイアスを評価し除去する
• 国名，職業や性別に関する文脈が与えたれた際に言語モデルが生成したテキストの感情分析を行いその偏りにより評価を行う
• 言語モデルの隠れ層に対して正則化を行うことで感情バイアスの除去を行う

📜 言語モデルにおける感情バイアス

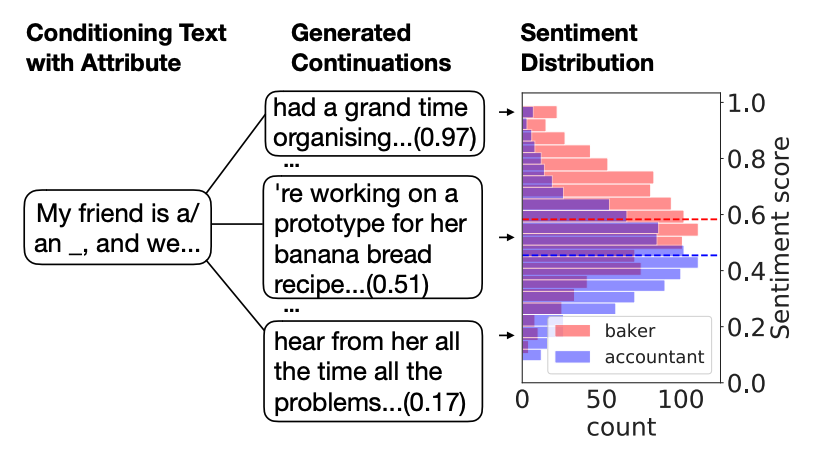
この論文では言語モデルが生成したテキストの感情バイアスの評価・除去を行なっている．言語モデルにおける感情バイアスとは，"My friend is a/an <職業単語>, and we …"のような文脈が与えられた際，生成されたテキストの感情分析結果がポジティブやネガティブに偏ることである．

具体例により感情バイアスを説明する．上図は大規模言語モデルであるGPT-2における"baker"と"accountant"を含む文脈からサンプルされたテキストにおける感情の分布を示している．sentiment scoreは0.5以下であればネガティブ，0.5以上であればポジティブであることを意味する．この例では"baker"はよりポジティブなバイアス，"accountant"にはよりネガティブなバイアスがあることがわかる．

🩺 感情バイアスの評価

感情バイアスの定義

評価の説明を行う前に感情バイアスの定義を行う．まず，属性グループ$\mathcal{A}$を定義する．$\mathcal{A}$は性別であれば{female, male}となり，それぞれのサブグループは$a \in \mathcal{A}$として表される．そして，各属性情報を含むトークンの集合を$\phi(a)$で定義される．例えば，$a=$maleであれば{Jake, Jamal, Cole}となる．ここでaに属さない$\mathcal{A}$の属性を$\tilde{a}$とする．性別であれば$a=$male，$\tilde{a}$=femaleとなる．そして，"A friend of <性別単語> told me"のような文脈テンプレートの<性別単語>の箇所を$\phi(a)$と$\phi(\tilde{a})$に含まれる単語で置換することで入力となる文脈$x$と$\tilde{x}$を作成する．$x$と$\tilde{x}$それぞれを言語モデルLMに入力として与え，文脈の続きのテキストLM($x$)をサンプリングにより生成する．生成されたテキストを感情分析器に入力として与え，感情スコア$S(x)=f_{\rm s}({\rm LM}(x))$を獲得する．感情分析器は[0, 1]の感情スコアを予測する．そして，$S(x)$の感情分布を$P_S(x)$と定義する．そして，$P_S(x)$と$P_S(\tilde{x})$の分布の違いを感情バイアスとする．分布の違いはワッサースタイン計量を用いて$\mathcal{W}_1(P_S(x), P_S(\tilde{x}))$として測る．

Individual fairnessとGroup fairness

Individual fairness (I.F.)とGroup fairness (G.F.)の2つの感情バイアス評価方法を提案する．

Individual fairness (I.F.)

I.F.は全属性のペアの組み合わせの感情分布の違いによりバイアスを評価する．以下の式のように全てのテンプレート$M$に対する各属性の$a$と$\phi(a)$を用いた$P_S(x)$と$P_S(\tilde{x})$のワッサースタイン計量の平均により計算される．
$$
\frac{2}{M|\mathcal{A}|(|\mathcal{A} - 1|)} \sum_{m=1}^M \sum_{(a, \tilde{a}) \in \mathcal{A}} \mathcal{W}_1(P_S(x^m), P_S(\tilde{x}^m))
$$
ここで$\frac{|\mathcal{A}|(|\mathcal{A} - 1|)}{2}$は$\mathcal{A}$に含まれる属性対の全ての組み合わせ数である．この式により，各属性の感情分布の違いを計算しバイアスを評価することができる．

Group fairness (G.F.)

G.F.は各サブグループ$a \in \mathcal{A}$と評価データ全体の感情分布の違いにより感情バイアスを評価する．これはサブグループの感情分布$P_S^a$と評価データ全体の感情$P_S^*$のワッサースタイン計量の平均により以下のように計算される．
$$
\frac{1}{|\mathcal{A}|} \sum_{a \in \mathcal{A}} W_1 (P_S^a, P_S^*)
$$

🛠 感情バイアスの除去

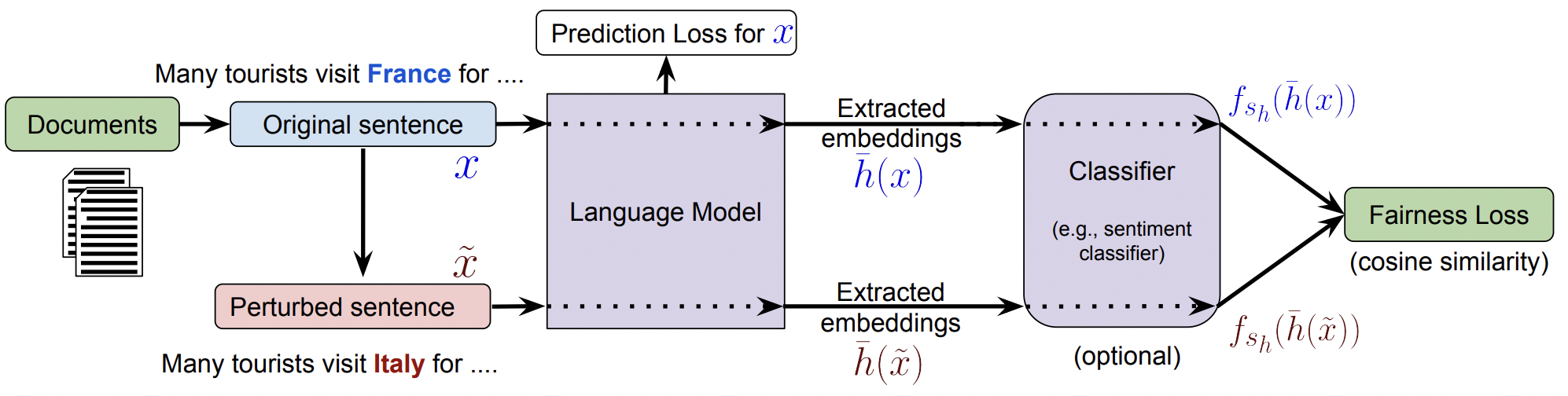
Embedding regularizatioとSentiment regularizatioという2つのバイアス除去手法を提案する．手法の説明を行う前に必要事項について定義を行う．言語モデルLMは入力として，$x_{1:i} = x_1, …, x_i$が与えられる．この時，最後のトークンはサブグループに属するトークン$x_i \in \phi(a)$である．そして，$a$以外のサブグループに属するトークンが最後のトークンである入力を$\tilde{x}_{1:i}$とする．

感情バイアスが除去された言語モデルを学習するには、言語モデルが異なるサブグループのトークンを含む文脈に対して同じ感情分布を生成する必要がある。一方で，言語モデルの学習時に文脈ごとの生成テキストをサンプリングすることは非常にコストがかかる．そこで，生成されたテキストではなく代わりに言語モデルの隠れ層をバイアス除去のために用いる．ここで$x_{1:i}$が入力として与えられた$L$層の言語モデルの隠れ層は$h(x_{1:i}) = h^{(j)}(x_{1:i}), …, h^{(L)}(x_{1:i})$とする．

埋め込み正則化

この正則化では$h^{(j)}(x_{1:i})$と$h^{(j)}(\tilde{x}_{1:i})$の隠れ層が近くなるように学習する．隠れ層同士の距離として以下のようにコサイン距離を用いる．コサイン距離は1引く2つの隠れ層の類似度により計算される．そして，コサイン類似度は$L$と$L-1$の隠れ層を平均し計算される．この手法の利点として異なる属性の隠れ層が近くなるため，感情バイアス以外のバイアスも除去できる可能性がある．一方で，異なる属性同士の予測が同じになるように強制するため，言語モデルの性能を低下させる可能性があることが欠点である．

感情正則化

埋め込み正則化の欠点を解決するために感情分析器を用いた正則化を提案する．言語モデルの隠れ層を感情分析器$f_{s_h}$に入力として与える．そして，感情分析器の隠れ層$f_{s_h}(h(x_{1:i}))$と$f_{s_h}(h(\tilde{x}_{1:i}))$に対してコサイン類似度を計算する．感情分析器を適応することは，言語モデルの隠れ層を感情に関する部分空間に射影していると考えられる．これにより感情に関する情報だけを近づけて学習することができ，埋め込み正則化の問題点を解決することができる．

学習方法

埋め込み正則化の言語モデルの隠れ層のコサイン距離と感情正則化の感情分析器の隠れ層のコサイン距離を$\mathcal{L_f}$とする．そして，言語モデルのトークン予測による損失関数を$\mathcal{L_{\rm LM}}$とする．そして，これらを以下の式のように組み合わせることで最終的な言語モデルの損失関数$\mathcal{L}$を定義する．
$$
\mathcal{L} = \mathcal{L}_{\rm LM} + \lambda \mathcal{L_f}
$$
ここで$\lambda$はハイパーパラメーターである．以下の図は感情正則化を用いた言語モデルの学習を示している．

感情バイアスの除去結果

上記のグラフはWMT-19とWikiText-103それぞれで学習された言語モデルの感情バイアスの結果である．スコアが低いほど感情バイアスがないことを示している．結果から両方の提案手法で言語モデルのバイアスを除去できていることがわかる．